Since former intelligence contractor Edward Snowden first began leaking classified information about the National Security Agency’s controversial online surveillance operations, the possibility for privacy in the Internet age has become an open question. At the forefront of that concern is encryption. As Snowden revealed back in September 2013, the NSA has done a considerable amount of work to gain backdoor access through the encryption schemes that protect much of the world’s Internet traffic.
So can anything be done to keep that information secure?
One lingering uncertainty in the future of encryption is quantum physics. It has already been proven that when the quantum computer is realized it will be able to easily break RSA encryption, one of the fundamental means of protection for bank transactions as well as many other forms of communication online. (Why will quantum computers make short work of RSA? Here’s a brief explanation.)
Reading that, it’s tempting to think quantum computers spell the end of encryption. And, considering Snowden’s leak that the NSA is working on a quantum computer, that fear isn’t entirely unfounded. However, quantum physics may offer hope for privacy advocates as well. Some scientists believe quantum cryptography may soon offer Internet users privacy protections that even the NSA won’t be able to skirt.
Understanding how this works requires a brief aside about asymmetric encryption. If Alice wants to send Bob a message, Bob must give Alice a key for encrypting the message. A simple real-world analog to such a key would be the direction to “advance each letter by one,” so the message “Hi Bob” would become the gibberish “Ij Cpc” while in transit. Because Bob has a key that says subtract one from each letter in Alice’s message, he can decode it once it arrives. The problem is, third parties like the NSA can intercept the key when Bob sends it to Alice, and with it can decode Alice’s private message to Bob without either of them ever knowing.
Quantum physics may offer an elegant solution. A bit in a classical computer has only two states, 0 and 1. But a quantum bit, or q-bit, can have many possible states at the same time. This is called superposition. And more curiously (and most importantly for our purposes), the act of measuring a q-bit’s state forces these many possible simultaneously occurring states into exactly one state. In other words, the act of measuring a q-bit necessarily alters it. (If this sounds familiar, that’s because it’s based on the same idea as Heisenberg’s Uncertainty Principle.)
Take an electron. “An electron has spin,” Berkeley mathematician Edward Frenkel told me. “It can spin in one direction or the opposite direction. Think of 1 and 0 as spin up and spin down.” At any given time, an electron has many possible states, each with a different probability of occurring. But, when someone measures it, “they have to force it,” Frenkel said, in this case into either 0 or 1. This means all of those other simultaneous states occurring with different probabilities are lost. (A rough analog to this information loss would be imaging what happens to a three-dimensional object when you flatten it into two dimensions.)
How does this apply to encryption? Say when Bob sends his encryption key to Alice, he uses quantum encryption. When Alice gets the key, one of two things will have happened. Either someone like the NSA will have intercepted it or it will be untouched. If the former occurs, then the key will be altered. This is because once someone measures the q-bits’ states, the q-bits will lose all of the information about their probable simultaneous states. So when the NSA then sends the key on to Alice and she measures it, it will be altered. Quantum cryptography destroys keys after they are read, carrying with them a 21st century “burn after reading directive.”
In the simplest terms, you can’t read the same key twice.
In order to determine whether or not the key has been intercepted, Alice could simply call Bob and check a relatively small number portion of the key. She wouldn’t need to be on a secure line either, as she would need to check very few bits before she could be almost certain, mathematically, that the key was untouched. (If it was altered, it would be useless to her, the NSA, and Bob.) “Eavesdropping,” said Frenkel, “would be impossible.”
Here’s a flow chart that shows, in very simplified terms, how Alice might send Bob a message using quantum cryptography.
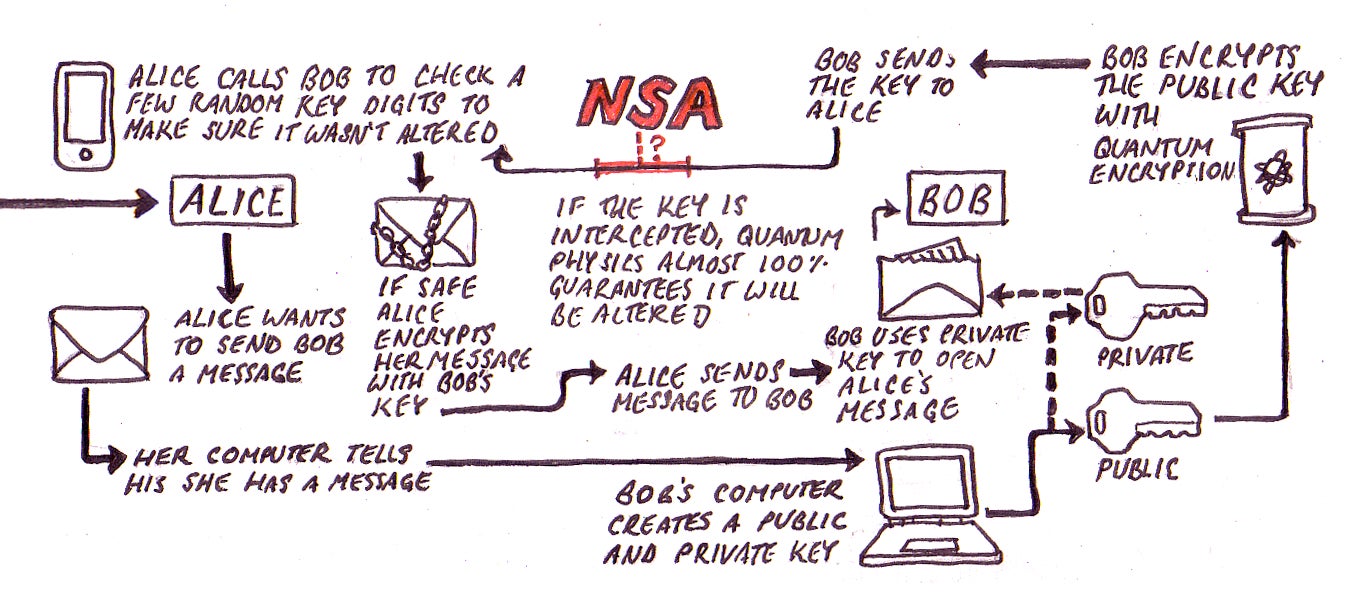
Illustration by Joe Kloc. Click here for full-size view.
For Frenkel, quantum cryptography would be “a perfect everyday system.” But not everyone agrees. Security expert Bruce Schneier told me it was “not at all news, or even a big deal.” As Schneier pointed out, the concept has been around since the 1980s. He feels it fails to address the main security issues facing cryptography.
As he wrote in Wired, “Cryptography is the one area of security that we can get right. We already have good encryption algorithms, good authentication algorithms and good key-agreement protocols. Maybe quantum cryptography can make that link stronger, but why would anyone bother? There are far more serious security problems to worry about, and it makes much more sense to spend effort securing those.”
“The real problems are elsewhere,” he added, “computer security, network security, user interface and so on.” Indeed, Snowden’s leaks have revealed that the NSA didn’t crack math problems or intercept keys to break internet encryption, but brokered deals with companies and sewed loopholes into encryption schemes.
But if nothing else, quantum cryptography stands as an enticing example of how physics may one day add a new, quantum component to mathematical cryptography. As Schneier wrote, “the basic idea is still unbelievably cool.”
How RSA encryption works: RSA encryption is based on the fact that if you take two very large prime numbers (that is, numbers divisible only by themselves and 1) and you multiply them together, it will be very hard for someone else to determine what those original primes were from that number alone. In other words, there is no known speedy algorithm on today’s computers that can factor a large number into its prime components. However, such an algorithm is known for a quantum computer. It’s called Shor’s algorithm and with it, a quantum computer can make fast work of RSA.
Infographic by Joe Kloc | Main art by Jason Reed


